– Annotated Outline –
This post, again beginning with the identifier {Re:SYNx-Maps, where x=1to7}, follows our preceding posts, http://relatedone.blogspot.com/2008/05/mapping-new-virtual-relational-world.html and http://relatedone.blogspot.com/2008/06/mapping-new-virtual-relational-world.html and
continues the post at
MONDAY, JUNE 16, 2008
Mapping the NEW (VIRTUAL RELATIONAL) WORLD: Foundational/Formal/Theoretical RS Development Outline-Part I {Re:SYN1-Maps}
DEVELOPMENT
I. NOTIONAL FOUNDATIONS
II. GENERAL RELATIONAL THEORY CONSTRUCTION
 as THE FORM of a general [meta order(ing)] theory of theory formation with components—objects (specific SYSTEMS), operations (specific INTER-SYSTEMIC RELATIONS) and preferred order(ing) relations (specific SYSTEMIZING RELATIONS).
as THE FORM of a general [meta order(ing)] theory of theory formation with components—objects (specific SYSTEMS), operations (specific INTER-SYSTEMIC RELATIONS) and preferred order(ing) relations (specific SYSTEMIZING RELATIONS).NOTE ON FORMALIZATION
It is taken as a given that the development of a Formal Theory requires attention to all of the following Relations (R) and Systems (S). The brief outline of this present post, however, is only directed at identifying certain of the necessary RS’s and does not address completion of their organization nor attend to their sufficiency as a Formal Theory, although this is the immediate strategic intent of this research in the construction of a SPECIFIC RELATIONAL THEORY.
FORMAL (IMAGE) SYSTEM (FS)
- Specify primitive S’s and R’s
- Define how RS’s should be constructed from primitive S’s & R’s
- Presume certain primitive RS’s (axioms; postulates)
- Specify IaR (rules of inference) stating conditionally how other RS’s (theorems) are to be derived from the primitive RS’s.
- Certain RS’s shown to be explicit RS’s derivable by IaR from the primitive RS’s
- Meta-RS’s about the FS itself which relate certain of its parts in specified ways
IMAGE–>ACTIONAL RELATIONS (RELATIONS TO EXPERIENCE)
(1) ORDER Formalisms
In terms of ORDER formalisms, the Laws of Form [Spencer-Brown, G. (1969). Laws of form (4th ed.). New York: E. P. Dutton], built on the assumed notions of ‘distinction’ (Subsumption) and ‘indication’ (Image), advanced the foundational formulation of a mathematics of distinguishability (boundary mathematics) which was shown to imply a Boolean algebra (having an interpretation as Boolean logic-deductive reasoning-where implication is among logical assertions in situations of complete certainty=order) as one of its many consequences, and which has now been expanded to General MultiBoundary Formalisms (Lattices, Algebras, etc. (recognizing that every algebra has its arithmetic) and their associated Calculus) wherein
- A set of logical statements ordered by implication gives rise to a Boolean lattice (or a Boolean algebra), and
- The Boolean lattice of logical statements induces the free distributive lattice of questions (the question lattice or algebra).
FROM IMAGE AND SUBSUMPTION TO MATHEMATICS AND LOGIC
(AND SYNTHETIC INTELLIGENCE/MIND)
Although this brief formal snippet may at first seem opaque, it can be transparent (enlightening) to realize that by simply grasping the concept of “distinction” the world of mathematics and the formal theories constructed thereon, which are the core essence of the work addressed herein, are within an Occam Simple grasp.
The theme of this argument, following an editorial extraction by the authors from George Spencer-Brown, Laws of Form: Evolution of Consciousness, is that a universe comes into being when a space is severed by drawing a distinction. By tracing the way we represent such a severance, we can begin to reconstruct, with an accuracy and coverage that appear almost uncanny, the basic forms underlying linguistic, mathematical, physical, and the life sciences, and can begin to see how the familiar laws of our own experience follow inexorably from the original act of severance. The act is itself already remembered, even if unconsciously, as our first attempt to distinguish differences in a world where, in the first place, the boundaries can be drawn anywhere we please. (Spencer-Brown 1969)
The expectation here is simply for an “open” impression by the reader regarding the arguments herein; quite obviously, the inclusive argument can not be joined in this limited exposition. On the other hand the partial arguments here presented are “informative” when focusing attention on this open impression.
To introduce the Occam Simplicity of creating Formal Systems, we begin with Personal Experience of the Existence of The Form of Relational System (RS), but with only the Presumption of imaging Experience as an Essence thereof. Let this experience be imaged as that is, the Person (imaged as the observer “eye”) is within The Form of RS with no other essence. Let this existence be called (imaged as) the Void (or R-Space or more formally, a Potential RS). The Void is not a mathematical (i.e. a formal “RS”) or physical space, nor is it a “System” of any sort. It is the absence (Non-Existence) of any System, and thus it possesses no attributes of any kind, including emptiness. [For this insert, see generally Shoup, R. (2008). Boundary institute for the study of foundations. Retrieved June 17, 2008, from http://www.boundary.org/; referencing (Shoup 1994)]
that is, the Person (imaged as the observer “eye”) is within The Form of RS with no other essence. Let this existence be called (imaged as) the Void (or R-Space or more formally, a Potential RS). The Void is not a mathematical (i.e. a formal “RS”) or physical space, nor is it a “System” of any sort. It is the absence (Non-Existence) of any System, and thus it possesses no attributes of any kind, including emptiness. [For this insert, see generally Shoup, R. (2008). Boundary institute for the study of foundations. Retrieved June 17, 2008, from http://www.boundary.org/; referencing (Shoup 1994)]
Within the Void create (image) the simplest fundamental Essential Presumption as subsumption subsuming the notion of distinction. By drawing a distinction, we form a boundary with two sides, the first System in our Void (R-Space). We can visualize this first distinction by a closed curve (of arbitrary shape) in the plane as shown in Figure 1.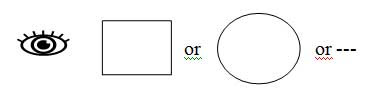
The distinction may be taken both as a System, e.g. an object (an area defined in the space), and as a Relation, e.g. an action (an injunction to cross from the outside to the inside). At this ultimately simple level, System and Relation as object and action or state and event or thing and change are united (undifferentiated) in a single concept, i.e. System and Relation are a Whole.
The functionality of the distinction may be seen more clearly when we draw a second distinction (Figure 2). Given a single object distinguished from the Void, only two possibilities exist for the second distinction: 2.a) as an additional identical distinction from the Void, or 2.b) as a distinction from (within) the existing object.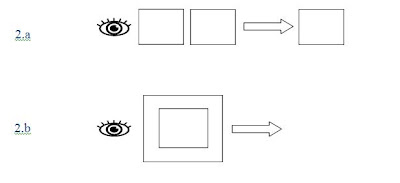
the axioms of the boundary mathematics (logic and arithmetic).
In the first case, we have two identical distinctions from the Void taken together, which is just the same as one distinction. (At this level of extreme simplicity, either we have distinction from the Void or we have not.) In the second case, a distinction from the first distinction (since there is no Other distinction) can only refer back to the Void. The second arrangement can also be thought of as a function — one distinction “applied to” or “surrounding” another. Using these two relations as axioms, any arrangement of boundaries (multiple distinctions including distinctions within distinctions) in the plane (Void) can be simplified to either one distinction or the Void.
The foregoing brief perspective on the mathematics of distinction has grown into a general candidate for an approach to a universal language for formal systems, MultiBoundary Mathematics. Inherent to this latter is a Boundary Logic from which Boolean Logic is derivable as a special case and which is leading to a more powerful computer design. [See generally Bricken, W. (2007). Boundary mathematics. Boundary logic. Retrieved June 17, 2008, from http://wbricken.com/index.html; referencing (Bricken 2002; 2004)] Generally, taking a universal formal system as an axiom system with the property that any other consistent axiom system can be interpreted within it, the mathematics of distinction implies a mathematics of subsumption which, in turn, implies a Membership theory as a first step towards a universal language for mathematics. [Etter, T. (2006), Three-place Identity. Private Publication. Saratoga, CA.: Boundary Institute]
(2) DISORDER Formalisms
NOTE: R.Elated’s RELATIONISM treats the notion of probability as being composed of a “subSystemic probability” (to be referred to herein as “probability” in the lower case) which corresponds to the classical Bayesian understanding as foundationally grounded by Cox (see below) and a “Systemic probability” (to be referred to herein as “PROBABILITY” in the upper case) which, in one instance, corresponds to the generalized entropy of Cox as a measure of relevance in the query algebra (also see below). When referring generally to the notion of probability, “Probability” will ordinarily be used; however, the reader may have to rely on the context since the author’s diligence in this matter is expected to be frequently deficient.
To gain true understanding in any area of study, the foundations need to be repetitively re-explored. Cox’s investigations into the role of consistency of probability theory with Boolean algebra were a crucial initial step in this new exploration. The Algebra of Probable Inference/Inquiry (Cox, R. T. (1961). The algebra of probable inference. Baltimore, MD: Johns Hopkins Press) has finally been recognized as the succinct and profound foundational form of formalized Probability in representing DISORDER.
The effect of Cox’s contribution to probability theory was to generalize Boolean implication among logical statements to degrees of implication represented by real numbers (NOTE: by varying the algebra and extending the number system, e.g., to complex or quaternion numbers, other formulations of Probability such as quantum probability arise), which are manipulated using rules derived from consistency with the Boolean (or other underlying) algebra. These rules are known as the sum rule, the product rule and Bayes’ Theorem, and the measure resulting from this generalization is “probability”.
Generalizing a particular function of the question lattice leads to a valuation called relevance, which is a measure of the degree to which a statement answers a given question. Cox conjectured that this degree can be expressed as a generalized entropy which has subsequently been shown to be the case.
For the foregoing part of this section as well as the next section see generally Fry, R. L. (2001), MaxEnt2001, Bayesian Inference and Maximum Entropy in Science and Engineering: 21th International Workshop at Johns Hopkins University, Baltimore MD (USA). August 4-9, 2000; AIP Conference Proceedings 617. May 2002. pp. 410-432. Edited by Robert L. Fry. Available at: proceedings.aip.org (volume 617), http://www.blogger.com/www.jhuapl.edu/maxent2001.
(3) REORDERING Formalisms
The method of Maximum Entropy Inference [Cox, R. T. ( 1979), “Of inference and inquiry, an essay in inductive logic,” in The Maximum Entropy Formalism, edited by R. D. Levine and M. Tribus, The MIT Press, Cambridge, 1979, pp. 119–167]; [See generally Jaynes, E. T. (2003), Probability Theory: The Logic of Science, Cambridge Univ. Press, Cambridge; 2003; including references (Jaynes 1957, 1968, 1979, 1985)] generalized to Optimum Systemic(SubSystemic) Probabilistic Inference (OS(sS)PI) [See generally Hamann, J. R. at http://www.relationalsystems.net and references therein (Hamann 1968, 1969a, 1969b, 1972)] within RELATIONAL SYSTEMS as the progenitor of the formal basis for REORDERING the DISORDER completes THE FORM.
It is now well-understood that probability theory is literally an extension of (deductive) logic. Integrating the logic of inference (probability) with the logic of inquiry (relevance=entropy) yields a powerful formulation of inductive reasoning (logic) when completed through the use of the Principle of Maximum Entropy for assigning prior probabilities since this maximizes the relevance of the parameterization of the subject system.
CONJECTURE: It is also speculated here, based on real, but partial evidence, that the third mode of reasoning, i.e. abduction, may be formalizable by invoking a MiniMax Entropy Principle. Formal inclusion of abduction is necessary to complete a system of automated, autonomous inquiry/inference/intuition. [Hamann, J. R. (2007). Computational autognomics: An introduction. In R. Gudwin & J. Queiroz (Eds.), Semiotics and intelligent systems development (pp. 287-309). Hershey, PA: Idea Group Inc.]
The third post (III) in this series Mapping the NEW (VIRTUAL RELATIONAL) WORLD: Foundational/Formal/Theoretical RS Development Outline-Parts I, II & III {Re:SYN1-Maps} will follow in the not too distant future.









Tue, Jul 22, 2008
R. ELATED MIND TRUST